阅读笔记 —— 《Manufacturing Resilient Bi-Opaque Predictates against Symbolic Execution》

概述

控制流混淆通过保持语义不变的转换来增加程序复杂性。不透明谓词是实现这种转换的基本工具。然而，我们观察到现实世界中的不透明谓词通常非常简单，并且考虑的安全性很少。最近，这些不安全的不透明谓词受到了基于符号执行的对手的严重攻击，危及了控制流混淆的安全性。因此，本文提出了可以抵抗基于符号执行对手的符号不透明谓词。我们设计了一个通用框架来组合这种不透明谓词，该框架需要在每个不透明谓词中引入具有挑战性的符号分析问题（例如符号内存）。通过这种方式，我们可以误导符号执行引擎得出错误的结论。我们观察到关于符号不透明谓词的一种新颖的双重不透明特性，这不仅会导致对攻击者的误报问题，还会导致漏报问题。为了评估我们想法的有效性，我们基于Obfuscator-LLVM实现了一个原型混淆工具，并对实际程序进行了实验。我们的评估结果表明，符号不透明谓词对流行的符号执行引擎（如BAP、Triton和Angr）表现出优异的抗性。此外，虽然符号不透明谓词的成本可能因不同问题设置而异，但某些谓词可能非常高效。因此，我们的框架既安全又可用。用户可以遵循该框架，将符号不透明谓词引入他们的混淆工具中，使其更强大。

双重不透明谓词构造

命名了两种类型的不透明谓词：

1. I型不透明谓词：假阴性不透明谓词

   对手未能检测到模糊谓词，错误地将它们识别为正常谓词。换句话说，混淆的控制流图中的模糊谓词未被识别出来。

2. II型不透明谓词：假阳性不透明谓词

   对手错误地将正常谓词识别为模糊谓词。换句话说，正常的控制流图中的某些谓词被误认为是模糊的。

接下来是介绍几种不透明谓词构造的方法，这些方法利用符号执行的弱点来组成不透明的谓词，这样它们就可以逃避基于符号执行的检测。

符号内存难题

符号内存是程序分析中的一个难题，因为它涉及指针分析问题。下图是一个示例。

在这个例子中，构造了两个整数数组。符号值 j%7 指向第一个数组中的一个元素，该元素作为第二个数组的偏移量。然后从第二个数组中选择的元素被赋值给一个新变量 i。通过这种方式，i 是一个受符号内存难题保护的符号值，我们可以用 i 来构造符号模糊谓词。

例如，我们可以构造一个不能被满足的类型I模糊谓词，如 i == j。使用这个模糊谓词，我们可以插入一个虚假的代码块（即 Bogus()），它永远不会被执行。这个谓词的安全性取决于符号执行引擎的能力。如果符号执行引擎没有处理符号内存的机制，它将生成错误的约束模型，并错误地将这个谓词识别为普通谓词。

为了构造一个类型II模糊谓词，我们首先选择一个普通谓词，例如 j == 7。然后我们通过引入一个与 i 相关的新条件来修改这个谓词，例如 i == 1 && j == 7。这个修改不会改变原始谓词的语义，因为当 j 等于7时，i == 1 总是为真。这种条件可以很容易生成，因为 i 的值可以从任何 j 计算出来。在汇编代码中，新谓词将被解构成两个谓词 i == 1 和 j == 7。只有当第一个谓词为真时，第二个谓词 j == 7 才会被评估。如果符号执行引擎不支持符号内存，它将无法解决 i == 1 的约束，也无法达到普通谓词 j == 7。

通用模板生成算法

浮点数计算问题

浮点数用于表示实数近似值的一种数值格式，因此它的精度不准确。基于这一问题，浮点数会对符号执行带来麻烦。由于符号执行引擎在处理浮点数时，必须对浮点数背后的数学概念进行推理，而浮点数和有理数、实数之间的精度和表示方式存在差异，这可能会导致符号执行引擎在分析过程中出现不一致的结果或错误。

上图是一个利用该问题混淆的示例。在这个例子中，因为浮点类型不能精确表示0.1，所以无论我们给 symvar 赋什么值，f == 0.1 都不能满足。为了构造一个类型II谓词，我们可以将谓词 j == 7 改为 (1024 + f == 1024) && (f > 0) && (j == 7)。新的谓词旨在欺骗符号执行引擎，使其认为约束 (1024 + f == 1024) && (f > 0) 不能被满足，这在实数域中是正确的。然而，它在浮点数域中是可以被满足的。例如，f = 0.000007 是一个解。通过这种方式，当 j = 7 时，类型II模糊谓词可以被满足，从而保持语义。如果符号执行引擎不能处理这样的浮点数，它可能会错误地将 f == 0.1 视为普通谓词，而将类型II谓词视为模糊谓词。

隐蔽传播挑战

符号执行需要精确跟踪符号值的传播。然而，符号值可能通过许多方式传播，如输入/输出(I/O)操作。

在这个例子中，符号值 j 通过磁盘上的文件传播，然后赋值给 i。我们可以构建一个类型I不透明谓词 i != j，这将始终为假。如果符号执行引擎无法跟踪这种传播，它会将 i 视为一个常量，并将不透明谓词视为正常谓词。为了构建一个类型II不透明谓词，我们可以将谓词 j == 7 改为 i == 7，其中 i 等于 j。这种修改保持了程序的原始语义。然而，符号执行器可能会将 i 视为常量，从而得出错误的结论。

并行计算问题

并行程序（例如多线程、多进程）对于符号执行来说很难处理，因为执行顺序不仅由程序决定，还受主机计算机的影响。因此，我们无法为程序生成静态控制流图，而这是经典符号执行工作的基础。

在这个例子中，我们创建了两个额外的线程来修改符号变量 j 的值：一个线程将 in 增加 1，另一个线程将 in 减少 1。由于并行执行，两个线程同时对 in 的相同值进行计算。i 的值由最后终止的线程决定，在我们的例子中应该是第二个线程。最终，ThreadProp 函数的返回值应该等于 j - 1（Inc的tid被Dec的tid覆盖，最终仅执行Dec）。基于受保护的符号变量 i，我们可以构造一个类型I不透明谓词 i == j，以及一个类型II不透明谓词 i == 6。

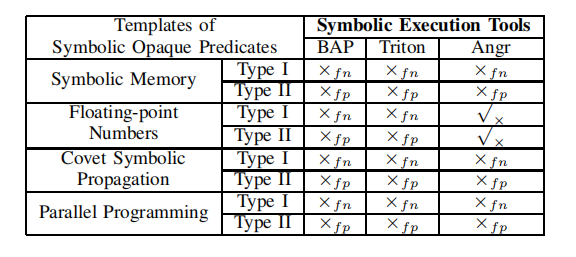
评估表