阅读笔记 —— 《改进的基于底层虚拟机混淆器的指令混淆框架》

改进

该论文对于LLVM-IR层的混淆进行了如下两种改进：

1. 指令加花
2. 指令替换

指令加花

该论文提出了两种指令加花方法：

1. 叠加跳转
2. 虚假循环

以上花指令以基本块形式进行添加，首先需要对原有的基本块进行拆分，然后在拆分后的基本块之间插入构造的花指令基本块，并通过不透明谓词进行有效的整合。

基本块拆分算法

算法1 Dependency Analysis Algorithm。
输入 instList ← instruction set in the basic block；
输出 resStack ← instruction dependency analysis results。
while instList.size > 0 do
    inst ← instList.getLast()
    stack.add(inst); queue.add(inst)
    while queue.size > 0 do
        toAnalyzeInst ← queue.pop()
        depInst← searching forwards for instructions that 
        toAnalyzeInst depends on in the instList
        stack.add(depInst)；queue.add(depInst)
        instList.remove(depInst)
    end while
    resStack.add(stack)
end while

​ 算法 1 的输入为基本块内所有的 LLVM-IR 指令，输出为存储指令依赖分析结果的嵌套堆栈集合，集合内的每一个子集也是一个栈，用于存储一组相互依赖的指令。算法实现的中间过程需要借助栈和队列来完成，前者用于存储相关依赖指令，最后作为子集存储到依赖分析结果集中；后者用于存储当前指令搜索过程中涉及的直接依赖指令和间接依赖指令，并不断向外扩展，直到没有新的依赖指令。针对每一条新加入的指令，均需要备份并对其依赖关系进行重新检查，通过队列实现每一条加入的新指令，其依赖的指令也会同步加入指令堆栈中。在指令依赖关系分析过程中，若出现所依赖的指令已经添加到其他的指令集合中，则生成原生指令的备份存储到新的集合中，以避免数据流的断裂问题。

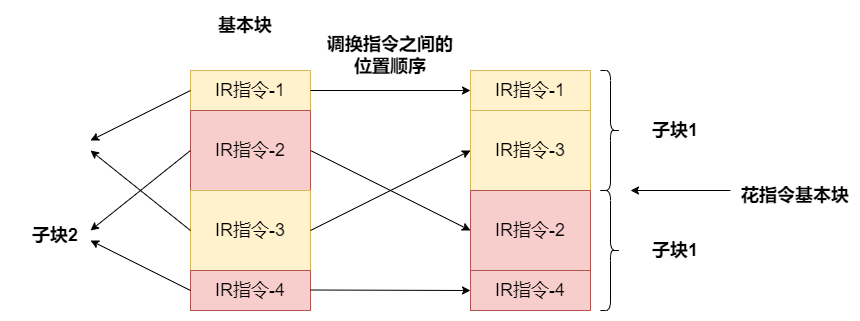
这里我就冒出了个问题，假如确定了基本块中的子块，但指令分布如下图左侧所示，那么怎么确定花指令的位置呢？或者说怎么用子块之间的特征来确定花指令的插入位置？（总不能是指令比对吧？毕竟指令之间的相似性可能会很大）

后面我想到了一个解释。既然这些指令之间没有数据关联性，那么其在执行顺序上理应也没有相关性，也就是说，我们将这些调换这些指令的位置顺序，使属于同一基本块的指令在位置上是连续的，如下图右侧所展示的。如此一来，基本块拆分后的子块之间的界限也就明显了，那么花指令的插入就可以在这些地方进行。

叠加跳转

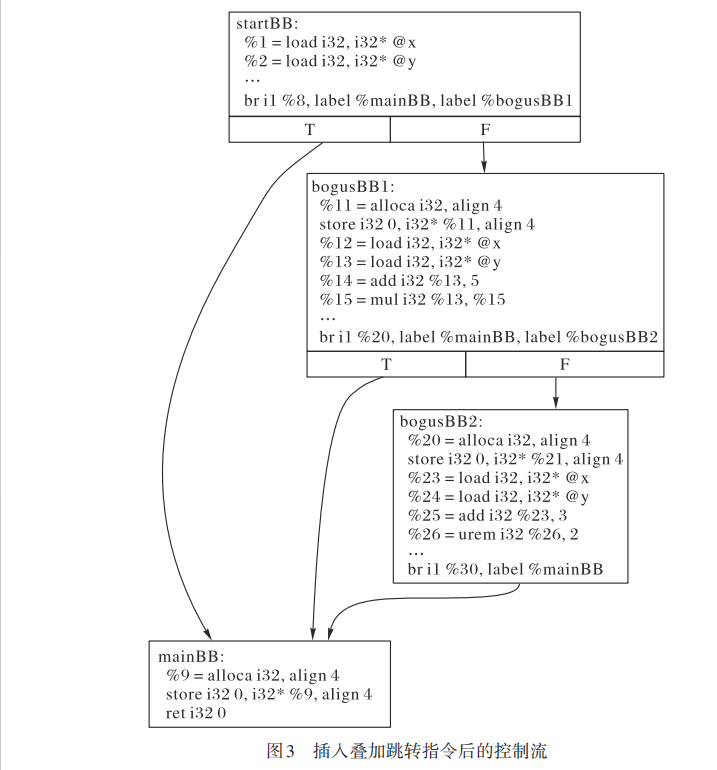
叠加跳转的示例如下：

虚假循环

定义循环基本块集合为loopBBs , loopBBs = {entryBB, loopCondition, loopBody}。

示例：

int i = 0;
int bound = 10;
while(i < bound){
	i += 1;
}

在上述代码中，entryBB对应第1、2行，loopCondition对应第3行，loopBody对应第4行。

基于上述定义，生成虚假循环体，为了与源程序有着数据相关性，可以在循环体内添加源程序中相关变量的运算操作，在循环条件中引入源程序中的变量等。

指令替换

指令替换混淆是指令的等效替换，即用语义相同但形式不同的一条或多条指令来替换。

该论文主要是对运算操作进行了混淆，例如对+、-、*、&、|、^、位移等运算进行等价替换，部分如下表所示：

运算符	等价指令序列
a=b+c	a=b-(-c)
a=b&c	a=(b^!c)&b
a=b|c	a=(b&c)|(b^c)

除此之外，还增加了两种替换方法：

1. 数据拆分替换
2. 循环替换

这两种方法只支持整数类型的变换。

数据拆分替换

数据拆分替换的定义如下：

程序的运算操作集记为 $O$， $O$所涉及的常量和变量集合记为 $D$，$Δx$记为运算中产生的进位或借位信息。对 $∀N ∈ D$，将$N$拆分为高位数据$N_{high}$和低位数据 $N_{low}$，$∀o∈O$转变为针对$N_{high}$和 $N_{low}$的操作，并同步更新$Δx$的数值，默认为 0。

示例：

循环替换

循环替换的目的主要是对操作符进行降级处理。它的定义如下：

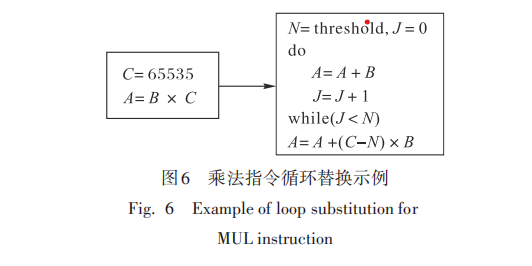
记操作的阈值为 $N$，操作 $Op1$为将程序中的左移指令转变为循环形式的乘法指令，操作 $Op2$ 为将乘法指令转变为循环形式的加法指令。使用 $Op1$ 或 $Op2$对 $∀i ∈ { inst|inst ∈ {MUL，SHL}}$进行处理，若循环的处理次数超过阈值 $N$，阈值内的循环逻辑保留，超出的部分仍使用之前的指令形式。

示例：

个人认为可以改进的地方

1. 对于运算操作的混淆，我认为可以使用快速乘、快速幂来替换乘、指数运算，这样一来，不仅达到了混淆，而且在时间开销上也降低了。
2. 对于有限小数的运算混淆，可以转换成整数运算的混淆，即将小数部分视为整数$*10^{-n}$。

疑问

• 基本块是什么？或者说怎样的指令集被认定为基本块？