格密码学习(一)
最近几天学习了格密码,于是写篇博客记录一下,当然其中不乏一些本人的错误理解,还望多多指正,感谢!
在讲格之前,先了解一下基向量和矩阵。
基
学过线性代数应该知道,一组基是由各个线性无关向量组成。
例如在直角坐标系中,任何一个向量都可以由(1,0)和(0,1)这两个向量任意组合而成,那么称这两个向量为基底向量。
三维空间中,基底向量为(1,0,0)和(0,1,0)和(0,0,1)。
扩展到n维空间,就有基底向量(1,0,0,……,0),(0,1,0,……,0),……(0,0,0,……,1)。
当然基底向量并不是唯一的,只要是一组线性无关向量,并且满足空间中任一项量能由该组向量表示,就可以称为基向量。
矩阵
矩阵可以理解为一组向量的集合,即矩阵$$A = \{\vec{i_1},\vec{i_2},……,\vec{i_n}\},$$$\vec{i_j}$为m维向量,$j∈[1,n]$。
$$
A =\left[\matrix{\vec{i_1}\\vec{i_2}\\…\\vec{i_n} }\right]
=\left[
\matrix{
a_{11}&a_{12}&…&a_{1m}\\
a_{21}&a_{22}&…&a_{2m}\\
\\…&…&…&…\\
a_{n1}&a_{n2}&…&a_{nm}\\
}\right]
$$
格
格可以理解为n维空间上的基向量的线性组合,仍可认为是一个向量,表示形式为矩阵。
举个例子:
格$L=\{a_1\vec{r_1}+a_2\vec{r_2}+…+a_n\vec{r_n}|a_i∈Z\}$,可表示为
$$
L =\left[\matrix{a_{1}&a_{2}&…&a_{n}\}\right]
\left[\matrix{\vec{i_1}\vec{i_2}\…\vec{i_n} }\right]
=\left[
\matrix{a_1\vec{r_1}+a_2\vec{r_2}+…+a_n\vec{r_n}}\right]
$$
但是,并不是所有的向量都是格。(这个有点不好表述)
例如,整数格如下所示:
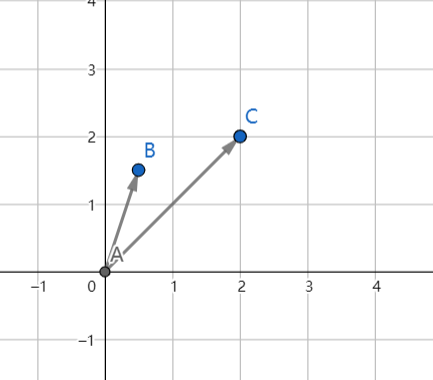
$\vec{AC}$是整数格,但$\vec{AB}$不是整数格。
可以把格理解为某空间中特定的点,例如只能是下图当中已标好的离散的点:
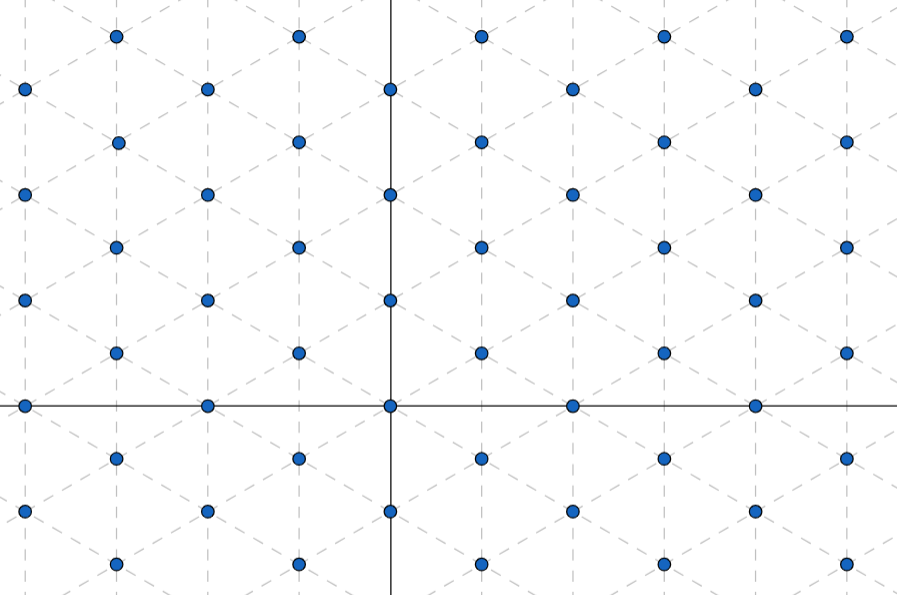
格的Determinant
格可以写成矩阵的形式,于是它的Determinant(行列式)代表其行列式的值,但一般不叫作行列式,而是组成格的向量所围成图形的面积或者体积。
最短距离
最短距离$λ$表示格中点与点之间的最短距离。
$$
λ_1 = min||\vec{x}-\vec{y}||,\vec{x},\vec{y}∈格L,\vec{x}≠\vec{y}\\
=min||\vec{x}||,\vec{x}∈格L,\vec{x}≠\vec{0},\vec{y}为原点o
$$
记$λ_i$为第i短的距离,则有$λ_1≤λ_2≤…≤λ_n$。
距离函数
任意一个点t(可以不在格L上)到最近的格点的最短距离的函数,记作$μ(t,L)$。
覆盖半径
以格L中所有的格点为圆心,逐渐扩大其半径,使得能覆盖整个空间,此时的半径就是覆盖半径$μ$。
格密码中的一些难题
最短向量问题(SVP)
给定格$L$中的一组基$B$,找到这组基构成的一个格点$Bx:x$,使得该格点到0坐标点的距离最近,即
$$
||\vec{Bx}|| = λ_1
$$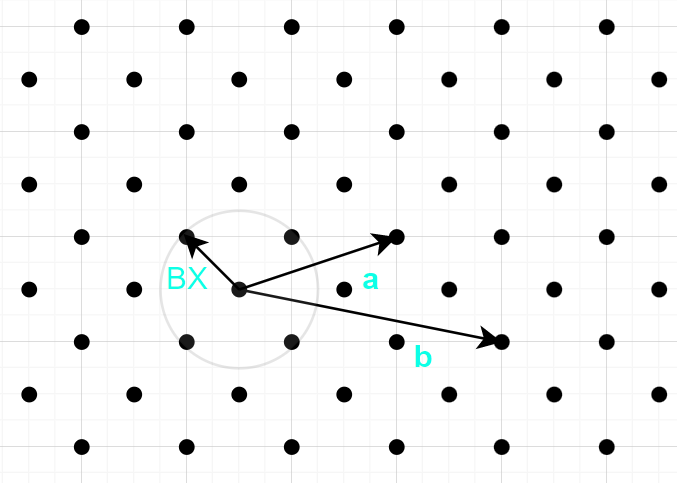
可以理解为找到一组整数$[x,y]$,使得新构成的向量
$$
\vec{Bx} =\left[\matrix{x&y\}\right]
\left[\matrix{\vec{a}\\vec{b}\}\right]
=x\vec{a}+y\vec{b}
$$
满足$||\vec{Bx}-\vec{0}|| = ||\vec{Bx}||=λ_1$。
最近向量问题(CVP)
给定连续空间中的任意一个点$\vec{t}$,在格空间$L$中找到一个格点$\vec{Bx}$,两点距离最短,即$||\vec{Bx}-\vec{t}||$最小,由覆盖半径定义可知,$||\vec{Bx}-\vec{t}||≤μ$。
利用格进行通信
根据CVP,假设我们信息加密后是格点$\vec{Bx}$,然后进行噪音干扰(可以理解为加了一个向量),变成了$\vec{t}$。这样别人就很难从$\vec{t}$破解出明文。
尝试分析CVP问题
由于CVP在笛卡尔坐标系整数格中很好求解,只需要向上或向下取整即可,因为该空间中的基向量都是互相垂直的。故在解决没有正交基的格中,我们将其基正交化,构造出正交基,并利用正交基划分格空间,使得每个格点都在长方形的正中心,
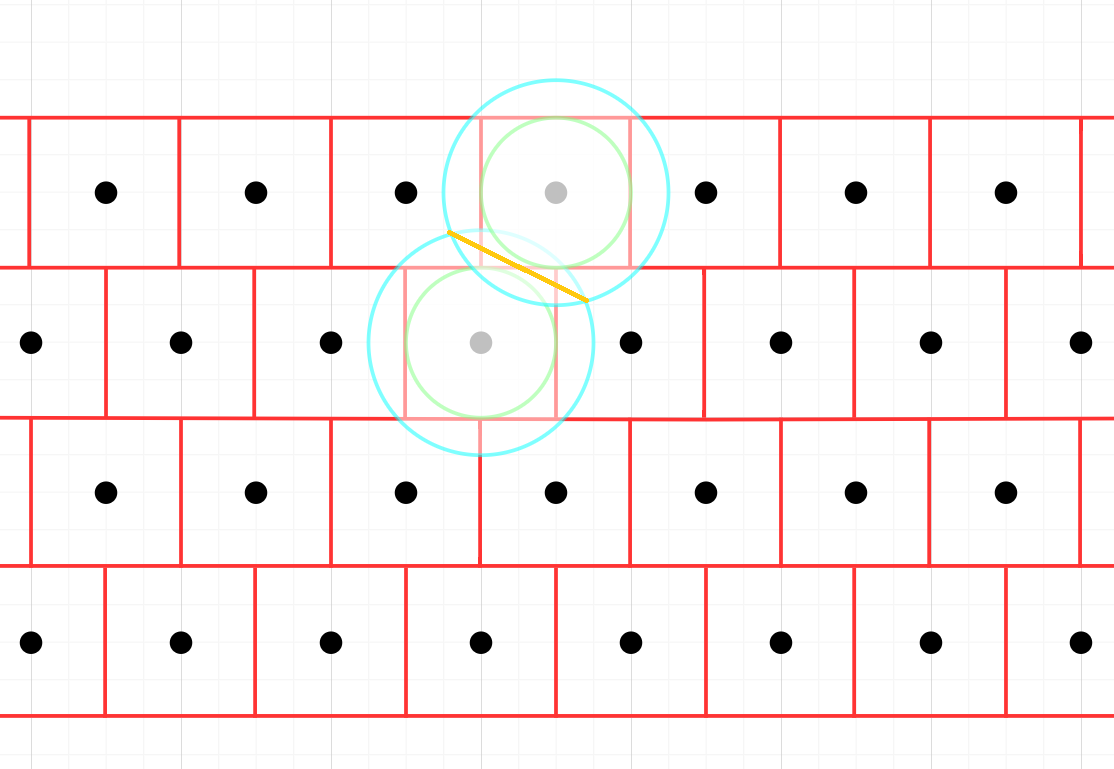
那么对任意一个非格点$\vec{t}$,求其最近向量为格点$\vec{Bx}$,它们之间的距离一定不会超过长方形对角线的一半。
从图中可以看出,在内圈中的非格点,其最近向量都在圆心处,但对于外圈中的非格点,可能存在多解问题(例如黄线上的某些点)
参考: