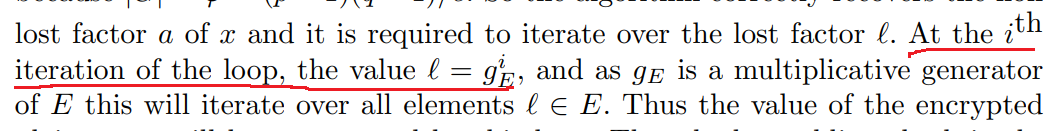SUSCTF2022

large case

from Crypto.Util.number import *
from secret import e,message


def pad(s):
    if len(s)<3*L:
        s+=bytes(3*L-len(s))
    return s

L=128
p=
q=
r=
n=p*q*r

assert isPrime(GCD(e,p-1)) and isPrime(GCD(e,q-1)) and isPrime(GCD(e,r-1)) and e==GCD(e,p-1)*GCD(e,q-1)*GCD(e,r-1)
assert len(message)>L and len(message)<2*L
assert b'SUSCTF' in message
m=bytes_to_long(pad(message))

c=pow(m,e,n)
print(c)

根据$e==GCD(e,p-1)*GCD(e,q-1)*GCD(e,r-1)$，设$e = e_pe_qe_r$。
$$
c≡m^{e_pe_qe_r}≡(m^{e_pe_q})^{e_r}\ mod\ n
$$
继而
$$
c≡(m^{e_pe_q})^{e_r}\ mod\ (r-1)
$$
根据费马小定理有：
$$
c^{(r-1)/e_r}≡(m^{e_pe_q})^{r-1}≡1\ mod\ (r-1)
$$
于是求得$e_r$，同理$e_p,e_q$也如此。

现在，我们求得了e，但gcd(e,(p-1)(q-1)(r-1)) = e，并不能直接解密，可以用AMM算法求解。

但这里根据官方题解用一个更快的方法。（算法来源：1059.pdf (iacr.org)）（稀里糊涂，英语水平有限，看不懂）

但满足如下条件：

由于该算法的时间复杂度为O(e)，即与e成线性关系，因此我们可以通过缩短e来缩短时间。

根据题目中$len(message)>L\ and\ len(message)<2*L$，而通过$pad$函数可以发现，message的填充部分>1024bit。因此可以将n缩小为pq，e缩小为$e_pe_q$。
$$
c ≡ m^{e} ≡ (m*2^{1024})^e\ mod\ n
$$
于是
$$
c_1 = c*2^{-1024e}≡m^e\ mod\ n
$$
简化模数
$$
c_1 ≡ m^e\ mod\ (p*q)
$$
这时候再将 $e_r$ 消除
$$
e_rd_r ≡ 1\ mod\ (p-1)*(q-1)\
c_0 = c_1^{d_r} ≡ m^{ed_r} ≡ m^{e_pe_q}\ mod\ (p*q)
$$
根据算法描述写出脚本：

第一步：寻找$g_E$。

第二步：找符合的明文

其中的$l$为$l=g_E^i$。

代码：

from Crypto.Util.number import *
import primefac
import gmpy2
import tqdm

p=127846753573603084140032502367311687577517286192893830888210505400863747960458410091624928485398237221748639465569360357083610343901195273740653100259873512668015324620239720302434418836556626441491996755736644886234427063508445212117628827393696641594389475794455769831224080974098671804484986257952189021223
q=145855456487495382044171198958191111759614682359121667762539436558951453420409098978730659224765186993202647878416602503196995715156477020462357271957894750950465766809623184979464111968346235929375202282811814079958258215558862385475337911665725569669510022344713444067774094112542265293776098223712339100693
r=165967627827619421909025667485886197280531070386062799707570138462960892786375448755168117226002965841166040777799690060003514218907279202146293715568618421507166624010447447835500614000601643150187327886055136468260391127675012777934049855029499330117864969171026445847229725440665179150874362143944727374907
c=2832775557487418816663494645849097066925967799754895979829784499040437385450603537732862576495758207240632734290947928291961063611897822688909447511260639429367768479378599532712621774918733304857247099714044615691877995534173849302353620399896455615474093581673774297730056975663792651743809514320379189748228186812362112753688073161375690508818356712739795492736743994105438575736577194329751372142329306630950863097761601196849158280502041616545429586870751042908365507050717385205371671658706357669408813112610215766159761927196639404951251535622349916877296956767883165696947955379829079278948514755758174884809479690995427980775293393456403529481055942899970158049070109142310832516606657100119207595631431023336544432679282722485978175459551109374822024850128128796213791820270973849303929674648894135672365776376696816104314090776423931007123128977218361110636927878232444348690591774581974226318856099862175526133892

for ep in primefac.primefac(p-1):#分解出p-1的所有因数
    if ep>2 and pow(c%p,(p-1)//ep,p)==1:
        break
for eq in primefac.primefac(q-1):
    if eq>2 and pow(c%q,(q-1)//eq,q)==1:
        break
for er in primefac.primefac(r-1):
    if er>2 and pow(c%r,(r-1)//er,r)==1:
        break

e=ep*eq*er
n=p*q*r
e0=ep*eq
n0=p*q
phi0=(p-1)*(q-1)
d1=gmpy2.invert(er,phi0)
c1=c*gmpy2.invert(pow(256,128*e,n),n)%n
c0=pow(c1,d1,n0)

g = 1
while 1:
    g+=1
    gE = pow(g,(p-1)*(q-1)//e0,n0)
    if gE != 1:
        break

#gE=pow(2,phi0//e0,n0)
d0=gmpy2.invert(e0,phi0//e0)
a0=pow(c0,d0,n0)
for i in tqdm.tqdm(range(e0)):
    m=long_to_bytes(a0)
    if b'SUSCTF' in m:
        flag=m.decode()
        print(flag)
        break
    a0=a0*gE%n0